Delphi’s System.Math.Vectors unit contains the TQuaternion3D class.
There is no information about the class in the Help so I post some code here so I remember how to use the class.
Following are some code snippets showing how to use quaternions to transform the mesh vertices in a model according to a skeletal hierarchy.
The procedures are used to build the models from old classic Tomb Raider games and export them to a 3D modelling program.
In Tomb Raider the animation data is stored as an (x,y,z) offset for the root bone and YXZ Euler angles for the rotations of all the bones.
In Tomb Raider a right handed coordinate system is used but the –Y axis is up so usually a further transformation is needed to get the models the right way up in other programs.
Here I do a 180 degree rotation about the X axis.
It is important to do this transformation last since then you don’t have to worry about adjusting the angles or offsets.
The code snippets also use System.Generics.Collections TStack and TList.
I also include a small example for the System.Math.Vectors TMatrix3D class which similarly has no Help topic.
Showing posts with label quaternions. Show all posts
Showing posts with label quaternions. Show all posts
Thursday, 3 May 2018
Tuesday, 8 July 2014
Keynote *.mqx file format
The Keynote plugin for Metasequoia stores its animation data in an XML text file with the file extension *.mqx.
I created the following simple animation using the Keynote plugin to study the keyframe data stored in the *.mqx file.
The animation starts and ends with both bones pointing in the +Y axis direction.

I created the following simple animation using the Keynote plugin to study the keyframe data stored in the *.mqx file.
The animation starts and ends with both bones pointing in the +Y axis direction.

Labels:
file formats,
Keynote,
Metasequoia,
quaternions,
skeletal animation
Mikoto *.mkm file format
Mikoto can export its animation data to a text file with the file extension *.mkm.
I created the following simple animation in Mikoto to study the keyframe data stored in the *.mkm file.
The animation starts and ends with both bones pointing in the +Y axis direction.

I created the following simple animation in Mikoto to study the keyframe data stored in the *.mkm file.
The animation starts and ends with both bones pointing in the +Y axis direction.

Labels:
file formats,
Mikoto,
quaternions,
skeletal animation
Monday, 7 July 2014
About Rotations in Skeletal Animation
In skeletal animation, for every frame of an animation, the position of a bone’s origin (pivot point) and a bone’s rotation is stored for each bone in a hierarchy of bones.
The hierarchy of bones is also known as a skeleton.
In this article I will only discuss the rotations.
Like any 3DCG object you create in 3D modelling software, each bone has a local coordinate system defined by X,Y and Z axes.
For example I can define a bone as an object where the direction from the origin of the bone to its tip is in the positive Z axis direction and the the top of the bone is in the positive Y axis direction.
In essence I have created an object as shown below.
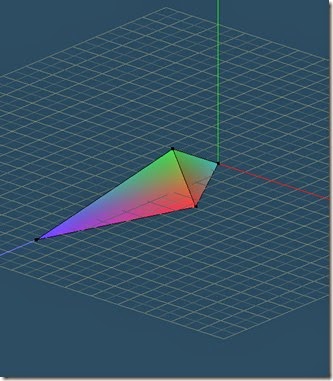
The hierarchy of bones is also known as a skeleton.
In this article I will only discuss the rotations.
Like any 3DCG object you create in 3D modelling software, each bone has a local coordinate system defined by X,Y and Z axes.
For example I can define a bone as an object where the direction from the origin of the bone to its tip is in the positive Z axis direction and the the top of the bone is in the positive Y axis direction.
In essence I have created an object as shown below.

Labels:
3D modelling,
quaternions,
rotation,
skeletal animation
Monday, 30 June 2014
Tip for Quaternion Multiplication by Hand
Here is a technique for multiplying two quaternions by hand so you do not have to remember the formula mentioned in my introduction to quaternions post [link].
If you are multiplying P x Q where P and Q are two quaternions create a grid as shown below.
Write the first quaternion of the multiplication in a column on the left side of the grid and then write the second quaternion in a row at the top of the grid.
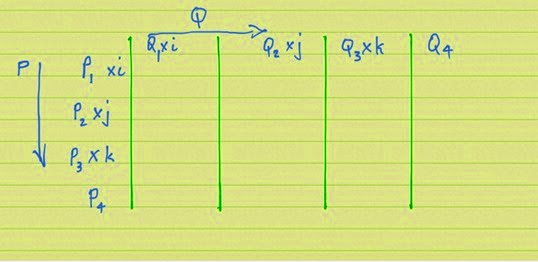
If you are multiplying P x Q where P and Q are two quaternions create a grid as shown below.
Write the first quaternion of the multiplication in a column on the left side of the grid and then write the second quaternion in a row at the top of the grid.

Saturday, 28 June 2014
A Gentle Introduction to Quaternions
The internet doesn’t have enough tutorials about quaternions so I thought I’d add another one. ;-)
You only need to learn the basic arithmetic and some formulae to enable you to get the hang of quaternions.
The multiplication sign, x in this article stands for ordinary, everyday multiplication.
Remember to to do the multiplications first in any sum before doing the additions.
Firstly I’ll introduce you to some unusual numbers that you don’t see in everyday life.
Lets call them alphabet numbers.
You only need to learn the basic arithmetic and some formulae to enable you to get the hang of quaternions.
The multiplication sign, x in this article stands for ordinary, everyday multiplication.
Remember to to do the multiplications first in any sum before doing the additions.
Firstly I’ll introduce you to some unusual numbers that you don’t see in everyday life.
Lets call them alphabet numbers.
Subscribe to:
Comments (Atom)